やはり落下傘の紐は全く役に立っていない。安井算哲のものと思しき解法で解いてみよう。
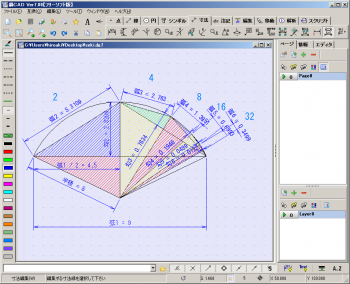
クリックすると拡大します
まず左側下、赤い直角三角形に注目
[勾下]= sqrt([半径]^2 - ([弧1] / 2)^2)
次に、左側上、青い直角形
[勾2] = [半径] - [勾下]
[弧2] = sqrt(([弧1] / 2)^2 + [勾2]^2)
従って、近似弧は
[近似弧] = [弧2] * 2
次に中央下、黄色い直角三角形に注目
[股] = sqrt([半径]^2 - ([弧2] / 2)^2)
次に、中央上、緑の直角三角形
[勾3] = [半径] - [股]
[弧3] = sqrt(([弧2] / 2)^2 + [勾3]^2)
従って、近似弧は
[近似弧] = [弧3] * 4
以下、気の済むまで繰り返せばよい。
ここで、Excel2010の仕様
ワークシートのサイズ: 1,048,576 行、16,384 列
有効桁数: 15 桁
処理できる負の最小値: -2.2251E-308
処理できる正の最小値: 2.2251E-308
処理できる正の最大値: 9.99999999999999E+307
処理できる負の最大値: -9.99999999999999E+307
数式によって処理できる正の最大値: 1.7976931348623158e+308
数式によって処理できる負の最大値: -1.7976931348623158e+308
数式の長さ: 8,192 文字
今回の答は11.なにがしだから、小数点以下13桁までは計算できそうだ。有効桁数: 15 桁
処理できる負の最小値: -2.2251E-308
処理できる正の最小値: 2.2251E-308
処理できる正の最大値: 9.99999999999999E+307
処理できる負の最大値: -9.99999999999999E+307
数式によって処理できる正の最大値: 1.7976931348623158e+308
数式によって処理できる負の最大値: -1.7976931348623158e+308
数式の長さ: 8,192 文字
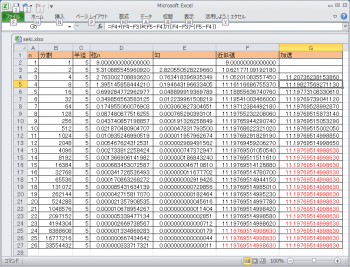
クリックすると拡大します
C列「半径」は、常に5。
D列「弦1」は、初期値9。
E列「勾n」は、式:5-sqrt(5^2-([弦(n-1)]/2)^2)
D列「弦n」は、式:sqrt(([弦(n-1)]/2)^2 + [勾n]^2)
F列「近似弧」は、式:[弦n] * [分割]
G列「加速」は、式:[近似弧(n-1)] + ([近似弧(n-1)] - [近似弧(n-2)]) * ([近似弧(n)] - [近似弧(n-1)]) / (([近似弧(n-1)] - [近似弧(n-2)]) - ([近似弧(n)] - [近似弧(n-1)])) ・・・ 関孝和の加速計算式
8388608分割すれば小数点以下13桁まで正しい答が得られる。ちなみに関孝和は32768分割まで計算して、加速式で精度を上げ、12桁で丸めている。関孝和の加速計算式、すごい。この問題だと4096分割で小数点以下13桁をクリアしている。このxlsxファイルは下に添付しておくので好きにして頂戴。
まさか、(映画)「天地明察」では、安井算哲が関孝和の加速計算式を使うなんて馬鹿なことやってないでしょうねぇ。facebook「映画『天地明察』ページ
んで?この問題、小数点以下何桁まで合っていれば「明察」なの?
添付ファイル: seki.xlsx















Comments