今有図如
大小方及日月円蝕交
大小方界相除シテ七分ノ三十寸
問日月蝕ノ分
この問題が「無術」となった原因は、「大小方界相除シテ七分ノ三十寸」にある。「長さ」割る「長さ」は「比率」なので単位はない。「寸」はおかしい。(ラジアンが微妙な立場なんだが・・・円周割る半径。んなもんで「補助単位」という半端な扱いを受けている。)それは置いといて、この条件を無視し、大円の半径を1(寸でもメートルでもいいんだが)として作図してみる。
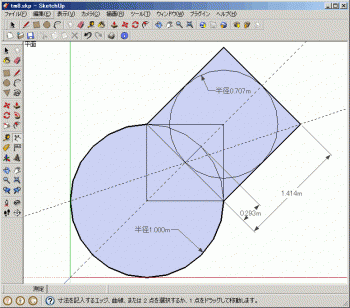
何のひねりもなく、1-(1/sqrt(2))≒0.292893219…であることがわかる。
これは、日半径=小方辺 という特殊な場合である。
日径を明示せず、大方、小方を固定した場合、蝕分は不定である。
冲方先生の解説を引用しておこう。
====以下「天地明察」第五版P159L7-L15引用
第一に、術を求めてゆくと、正と負の数の、複数の解答があり得た。昨今では、ときに算術において、複数の答えが導き出される場合があることは広く知られるようになっている。だがそれらは”病題”と呼ばれ、あくまで”一問一答”こそが算術の王道とされた。====以上引用
第二に、これは術そのものに矛盾を抱えていた。大小の方の辺の比は、春海が用意した答えでは偶数と奇数になる。そうでなければならない。だが小方と大方の比を求めてゆくと、にわかに矛盾が発生する。
大方の一辺は、すなわち小方の対角線であり、偶数である。そして小方の対角線は、奇数である。これらが同時に成り立ってしまう。奇数であると同時に偶数である。術を工夫すればするほどそうなる。完全な矛盾だった。なぜそんなことが起こったのか。
何の説明なのか、さっぱりわからない。sqrt(2)は整数ではないので、術を工夫しなくても、奇数でも偶数でもない。
日月があろうがなかろうが、大方界/小方界は、sqrt(2)であることは明白である。

30/7 ≠ sqrt(2)
∴無術
以上、終わり。
春海君が用意した答えが気になる。また、解答さんが何故斯様な問題を野放しにしたのかが腑に落ちない。
====以下「天地明察」第五版P156L9〜L12引用
日月の蝕交の分は、実は七と二十三の平方根を足して、四で割ったものになる、ということまで晴海は安藤に話した。七と二十三は足して三十。”七分の三十寸”にあくまでこだわった答えだった。だが、ただ七と二十三を足すのではなく、それぞれ開平させてから足させるところに自分なりの工夫と主張があった。====以上引用
・・・(絶句)かくして、更にどつぼにはまって行くのであった。














CID1272280255 ヌルハチ — 2010/04/26@20:10:55
a/b=√2 であるとする。ただし、a,bは自然数で a/b は既約分数。
a^2/b^2=2 より a^2=2*b^2
ここで、右辺は偶数だから左辺も偶数
つまり a は偶数
a=2*c とすると
4*c^2=2*b^2
2*c^2=b^2
したがって b も偶数
すると a も b も偶数となり約分できてしまい矛盾
よって √2 は有理数ではなく無理数
でも奇数うんぬんは関係ありませんね。